こんにちは。SCSKの山口です。
本ブログでは、前回のブログで作成したBigQuery MLの線形回帰モデルの性能を評価してみたいと思います。
[前回ブログ]モデル作成・予測結果

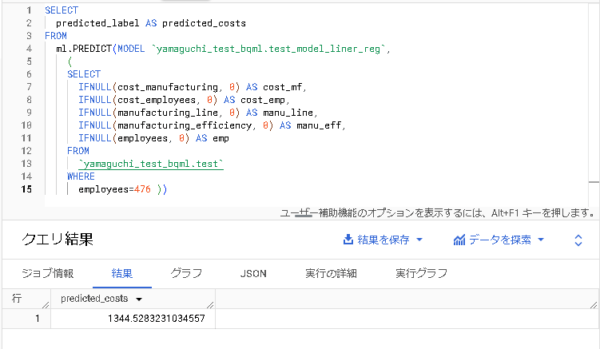
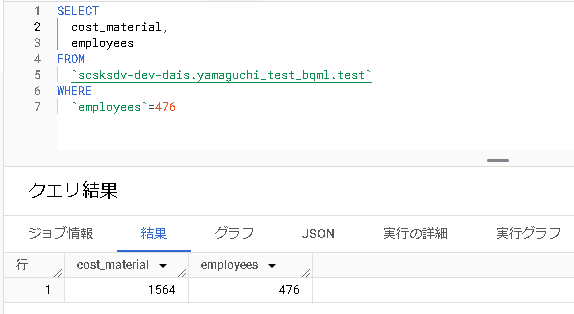
前回のブログで線形回帰モデルの作成・予測をした結果、下記の出力を得ました。
| 従業員数 | モデル予測結果(原材料費) | 正解値(原材料費) |
|---|---|---|
| 476 | 1344.5283231034557 | 1564 |
この結果は果たしてどうなのでしょうか、、?モデルの予測精度はどうなのでしょうか、、?
これを今回は計測したいと思います。
モデル評価

作成したモデルの評価は、「ML.EVALUATE関数」を用いることで可能です。
選択したモデルタイプによって、他の評価関数を使用することで様々な評価指標を得ることができます。詳細は公式ドキュメントをご覧ください。
今回はモデルタイプとして線形回帰を選択したので、ML.EVALUATE関数で評価してみます。
下記SQLを実行します。
SELECT * FROM ML.EVALUATE(MODEL `yamaguchi_test_bqml.test_model_liner_reg`, ( SELECT IFNULL(cost_manufacturing, 0) AS cost_mf, IFNULL(cost_material, 0) AS label, IFNULL(cost_employees, 0) AS cost_emp, IFNULL(manufacturing_line, 0) AS manu_line, IFNULL(manufacturing_efficiency, 0) AS manu_eff, IFNULL(employees, 0) AS emp FROM `scsksdv-dev-dais.yamaguchi_test_bqml.test` ));
| 実行結果 |
 |
公式ドキュメントを見ると、線形回帰のモデルでは、ML.EVALUATE関数を実行することで下記の指標が得られます。
- mean_absolute_error:平均絶対誤差
- mean_squared_error:平均二乗誤差
- mean_squared_log_error:平均二乗対数誤差
- median_absolute_error:絶対誤差の中央値
- r2_score:R2スコア
- explained_variance:説明分散
回帰モデルの評価指標
平均絶対誤差:MAE
平均絶対誤差(MAE)は、各行で[予測値 – 正解値]の絶対値(=絶対誤差)を取り、その平均を出したものです。
以下の式で表されます。
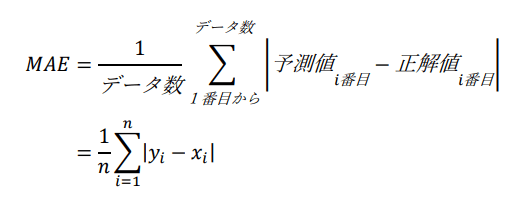
MAEの代表的な特性は下記のとおりです。
- 0以上の値
- 小さいほど良い結果となる
- 外れ値に対して脆弱
今回の結果で言うと、MAE=190くらいなので、「予測値と正解値が平均して190くらい離れている」ということになります。
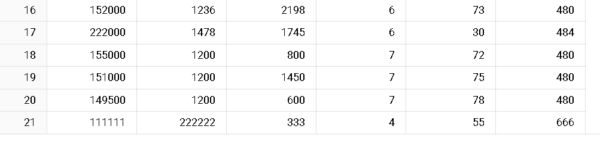
評価で使用したtestテーブルに外れ値を加えてMAEの値を見てみましょう。
21行目に原材料費が外れ値となるようなデータを追加しました。
この状態で再度モデルを評価してみると、
MAEの値がかなり大きくなりました。
このようにたった一つでも外れ値のデータが入ってしまうと値が大きくなってしまうのがMAEの弱点です。
平均二乗誤差:MSE
平均二乗誤差(MSE)は下記の式で表されます。
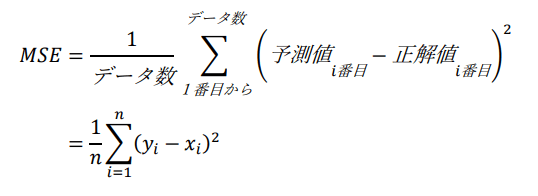
先ほどのMAEとかなり似た式ですが、予測値と正解値の差を二乗している点が違いです。
誤差を二乗しているため、より大きな誤差が発生していると値が大きくなります。すなわち、間違いをより重要視した指標ということになります。
この指標も値が小さいほど良い結果となります。
お気づきの方も多いかもしれないですが、MSEはMAEよりも外れ値に対して脆弱です。
誤差を二乗しているため、その分外れ値に対しても弱くなってしまうわけですね。
平均二乗対数誤差:MSLE
平均二乗対数誤差(MSLE)は、各行で予測値の対数と正解値の対数の差(=対数誤差)の二乗を計算し、その平均を出したものです。0に近いほど良い結果となります。
下記の式で表されます。
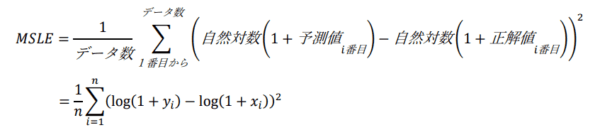
数学では、底が同じ対数の引き算は割り算に変換することができます。これに着目すると、上記の式は「予測値/正解値」の形に変換することができます。
すなわちMSLEは、予測値/正解値の比率に着目した指標であるということが言えます。
比率に着目することで、誤差が大きくなっても過大に評価しないことが可能です。
そのため、MAE,MSEの弱点であった、外れ値への脆弱性をある程度克服した指標と言えます。
絶対誤差中央値:MedAE
そのまま略すと「MAE」となり平均絶対誤差と混同してしまうので「MedAE」と略すのが一般的のようです。
MedAEは、各行で[予測値 – 正解値]の絶対値(=絶対誤差)を計算し、小さい順に並べた際の中央値を出したものです。
下記の式で表されます。
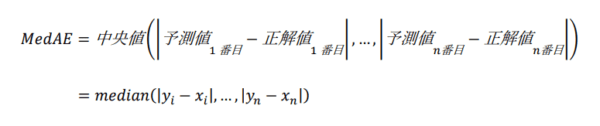
この値も、0に近いほど良い結果となります。
決定計数:R2スコア
R2スコアは、回帰モデルを評価する際に「最も直感的な基準」だと言われています・
これまで説明した指標はすべて誤差を見るものでしたが、ここでやっとモデルの性能(良し悪し)を測ることのできる指標が登場します。
複数のモデルの性能を比較する際にもよく使われる指標で、モデルがどれだけデータをうまく説明できているかを表現してくれる値です。
テストの点数に置き換えると理解しやすいです。
- 数学のテストの点数が高い:数学についてよく理解できており、説明できる。
- 英語のテストの点数が悪い:英語についてよく英買いできておらず、説明できない。
下記の式で表されます。

SSEとSSTについてみていきます。
残差平方和:SSE
- 各行に対して、観測値(正解値)と予測値の差を二乗した値を総和したもの
- MSEの平均を求めないバージョン
- 正解値と予測値がどれくらい離れているかを示す
二乗平均:SST
- 各行に対して、観測値(正解値)と全観測値の平均との差を二乗した値を総和したもの
- 分散の平均を求めないバージョン
- 正解データ自体の平均からのばらつき具合を示す
これを抑えたうえでr2スコアの公式をもう一度見ると、
予測値に正解データの平均値を用いた” 単純なモデル ”と” 作成したモデル ”を比較(前者で後者を割る)する
という作りになっていることがわかります。このことから、r2スコアは非常に単純なモデルと比較した際のパフォーマンスを示していると言えいます。
R2スコアは、1に近づくほど良い結果となります。
説明分散:EV
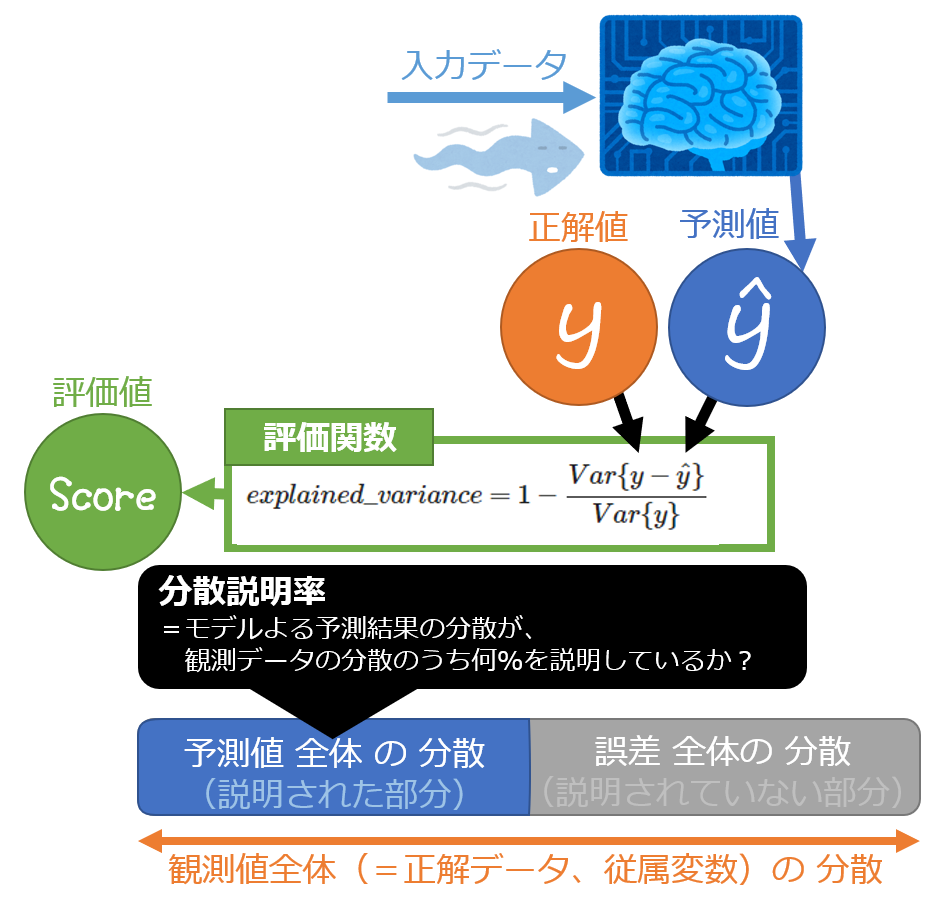
説明分散(ここではEVと略します。)は、R2スコアと同様にモデルの性能を測ることができる指標です。
正解データの散らばり(分散)のうち、モデルがどのくらいの割合を説明できるかを表現する指標です。
下記の式で表されます。

式のつくりを見ていきますが、視覚的に把握するために図式化します。
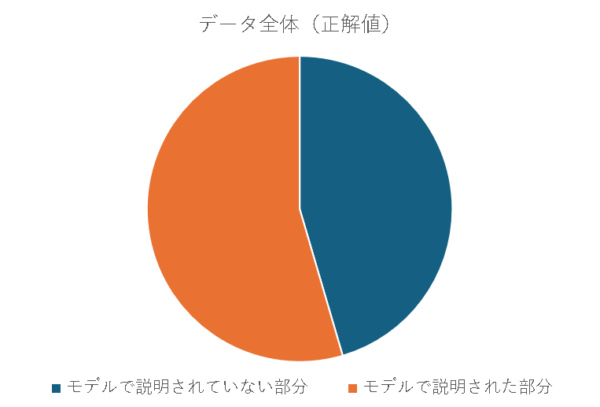
- オレンジ色:モデル予測できた割合
- 紺色:モデル予測できなかった(誤差)割合
です。
EV値では上図のオレンジ色の部分を以下の流れで表現します。

EV値は、1に近づくほど良い結果となります。
作成したモデルの性能はどうなの?
必要な知識が揃ったところで、今回作成した線形回帰モデルの性能を見てみたいと思います。
R2スコアとEV値を見てみると、
- R2スコア:0.568692977058064
- EV値:0.58093681298823574
という結果でした。だいたい60点くらいの性能のモデルですね。
まとめ
今回は線形回帰モデルを評価してみました。
複数の指標を組み合わせて評価することが非常に重要だと感じました。
ほとんど指標の説明に費やしてしまいましたが、今後はモデルの性能を向上させるための方法を調べてみたいなと思っています。