【GCP】BigQueryML ARIMA PLUSモデルで時系列予測してみる

こんにちは。最近BigQueryMLにハマっているSCSKの山口です。

もちろん今回もBigQueryMLに関するブログです。今回は時系列予測が可能なARIMA+（ARIMA PLUS）でモデルを作成し、実際に使ってみようと思います。

時系列予測をするにあたって様々な知識が必要になりましたが、今回はできるだけ漏れなく最低限まとめています。少し長いですが最後まで読んでいただけると幸いです。

筆者はこんな人です。
・Google Cloud歴：約2年
・BigQueryのコンソール操作には慣れている
・SQLが少し書ける
・AI/MLの知識はあまりない

時系列予測
1. 多変量時系列予測
実践
まとめ

時系列予測

読んで字のごとく。と言えばそこまでなのですが、せっかくなのでGeminiに聞いてみました。

時系列予測ってなんですか？

時系列予測とは、過去のデータの動きを分析し、将来の値を予測する手法です。例えば、過去の売上データから将来の売上を予測したり、過去の気温データから将来の気温を予測したりすることができます。

時系列予測の仕組み
時系列予測では、過去のデータに含まれるパターンやトレンドを捉え、それを未来に拡張することで予測を行います。

トレンド: データが長期的に上昇したり下降したりするような傾向のことです。
季節性: データが特定の周期で変動するパターンのことです。例えば、小売業の売上は季節によって大きく変動することがあります。
周期性: 特定の周期で繰り返されるパターンで、季節性よりも短い周期の変動を指します。
ノイズ: ランダムな変動で、予測を難しくする要因となります。

Geminiからの回答にもある通り、時系列予測は「過去のデータの動きを分析し、将来の値を予測すること」を指します。
ビジネス、経済、自然科学と幅広い分野で活用されています。

多変量時系列予測

BigQuery ML で多変量時系列予測を行う方法 | Google Cloud 公式ブログ

時系列分析の中でも今回は「多変量時系列予測」にフォーカスします。
多変量時系列予測は複数の変数間の時間的な関係をモデル化し、将来の値を予測する手法です。

単一の変数の動きだけでなく、複数の変数が互いにどのように影響を与えながら変化していくのかを分析します。
上記リンクではアイスクリームの売上を例に挙げられているのでそれになぞって説明します。

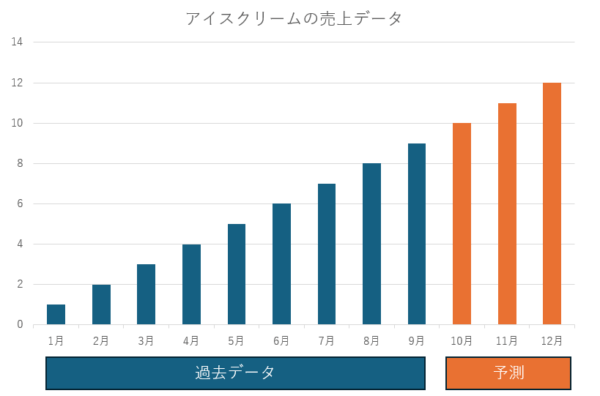
時系列予測で将来の売上データを予測する際、まず欠かせないのが「過去の売上データ」です。この情報だけでもある程度の予測はできます。たとえば上の図だと、1月～9月まで単調増加の傾向がみられるため、橙色の予測データように10月以降も増加するという予測を立てることができます。

ただ、寒くなり出す10月～12月にこれまで以上のアイスクリームの売り上げが望めるでしょうか、、、？

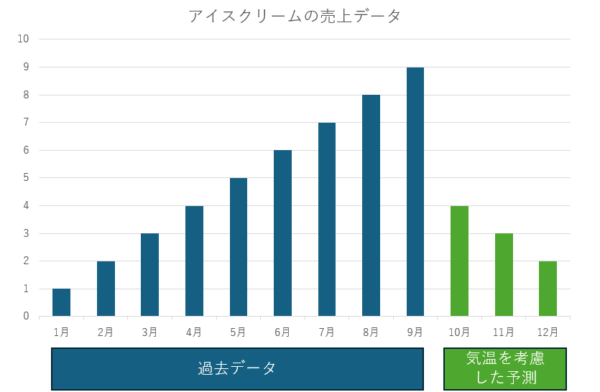
ここで「気温」という他の変数を考慮に入れてみましょう。
12月と比較的気温が近い1月のデータ等を考慮すると、寒くなる10月以降に関しては、下記のような予測ができます。

このように、「気温」という外部変数と「（過去の）売上」という目的変数を使用して予測をすることを「多変量時系列予測」と言います。

実践

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

今回は上記ドキュメントに沿って時系列予測（多変量時系列予測）をやってみます。

テーブル作成

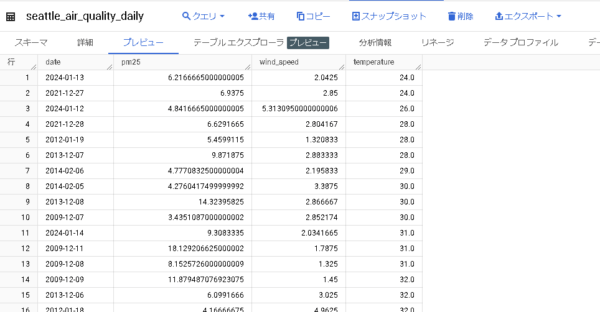
米国の複数の都市から日次で収集されたPM2.5、気温、風速の情報をもつepa_historical_air_quality データセットから、シアトルの情報を抽出したテーブルを作成します。

下記クエリでテーブルを作成します。

-- epa_historical_air_quality データセット内の *_daily_summary テーブルから各列を取得
CREATE TABLE `yamaguchi_test_bqml.seattle_air_quality_daily`
AS
WITH
  -- 各日の PM2.5 の平均値
  pm25_daily AS (
    SELECT
      avg(arithmetic_mean) AS pm25, date_local AS date
    FROM
      `bigquery-public-data.epa_historical_air_quality.pm25_nonfrm_daily_summary`
    WHERE
      city_name = 'Seattle'
      AND parameter_name = 'Acceptable PM2.5 AQI & Speciation Mass'
    GROUP BY date_local
  ),
  -- 各日の平均風速
  wind_speed_daily AS (
    SELECT
      avg(arithmetic_mean) AS wind_speed, date_local AS date
    FROM
      `bigquery-public-data.epa_historical_air_quality.wind_daily_summary`
    WHERE
      city_name = 'Seattle' AND parameter_name = 'Wind Speed - Resultant'
    GROUP BY date_local
  ),
  -- 各日の気温
  temperature_daily AS (
    SELECT
      avg(first_max_value) AS temperature, date_local AS date
    FROM
      `bigquery-public-data.epa_historical_air_quality.temperature_daily_summary`
    WHERE
      city_name = 'Seattle' AND parameter_name = 'Outdoor Temperature'
    GROUP BY date_local
  )
SELECT
  pm25_daily.date AS date, pm25, wind_speed, temperature
FROM pm25_daily
JOIN wind_speed_daily USING (date)
JOIN temperature_daily USING (date)

ARIMAモデル作成・トレーニング

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

それでは早速モデルを作成します。

-- pm25の量を予測するモデルを作成
CREATE OR REPLACE
  MODEL
    `yamaguchi_test_bqml.seattle_pm25_xreg_model`
  -- 外部回帰モデルの'ARIMA_PLUS_XREG'を作成
  OPTIONS(
    MODEL_TYPE = 'ARIMA_PLUS_XREG',
    time_series_timestamp_col = 'date',
    time_series_data_col = 'pm25')
AS
SELECT
  date,
  pm25,
  temperature,
  wind_speed
FROM
  `yamaguchi_test_bqml.seattle_air_quality_daily`
WHERE
  date
  BETWEEN DATE('2012-01-01')
  AND DATE('2020-12-31')

今回は「多変量時系列予測」が可能な「ARIMA_PLUS_XREG」をモデルとして採用しています。

上記クエリのOPTION句でモデルを指定していますが、デフォルトは auto_arima=TRUE が指定されています。これにより、auto.ARIMA アルゴリズムによって ARIMA_PLUS_XREG モデルのハイパーパラメータが自動的に調整されます。

auto.ARIMA

8.5 Non-seasonal ARIMA models | Forecasting: Principles and Practice (2nd ed)

2nd edition

auto.ARIMAはR言語のforecastパッケージに含まれる関数で、時系列データを自動的に分析し、最適なモデルを選定してくれるツールです。
auto.ARIMAを使用したトレーニングでは、最適な非季節順序（p,d,q）が自動的に検出されます。

非季節順序性

非季節順序性とは、ARIMAモデルのパラメータのうち、上記で記述した（p,d,q）で表される部分のことで、時系列データの非季節的な特徴を捉えるために使用されます。

	概要	解釈（大きい場合）
p：自己回帰次数	過去のデータが現在の値にどれだけ影響を与えるか	過去のデータが現在の値に与える影響が大きい
d：差分次数	データの非定常性を解消するために何回差分をとるか	データに強いトレンド性がある（＝トレンド性をなくすために多くの差分回数が必要だった）
q：移動平均次数	過去の誤差が現在の値にどれだけ影響を与えるか	過去の予測誤差が現在の値に与える影響が大きい

定常性は、データの動き方がどの時点でも一定である状態をいいます。

逆に、非定常性は、時間経過による影響でデータが上昇/下降の傾向を見せる状態を指します。

ARIMAモデル概要

Introduction to ARIMA models

ここでARIMAモデルについて詳しく触れます。
ARIMAモデルは以下の三つの要素で構成されます。

自己回帰（AR）項：過去のデータを予測変数として使用する。pで表す。
差分（I）項：データの定常化を行う。非定常性を解消するために実施した差分の次数。dで表す。
移動平均（MA）項：過去の予測誤差を予測変数として使用する。qで表す。

ARIMAモデルはこれらの用をの次数を組み合わせることで「ARIMA(p,d,q)」のように表記されます。

ARIMAモデルは下記手順で構築されます。

データ定常化：時系列データを定常化（非定常性を解消）する。I項の次数（d）を決定する
モデル識別：自己相関関数（ACF）と偏自己相関関数（PACF）を分析し、AR項、MA項の次数（p,q）を決定する
モデル推定：決定した次数に基づいてARIMAモデルを推定する
モデル診断：残差分析を行い、モデルの適合率を評価する

自己相関についてちょっと寄り道します。

「自己相関」とは、時系列データにおいて、異なる時点におけるデータ間の相関関係のことです。
つまり、過去のデータと現在（将来）のデータの間にどの程度関連性があるかを示します。これを視覚化したものが「自己相関関数」になります。

一方で、「偏自己相関関数」は何を指すのでしょうか。日々の売上データ分析を例に考えていきます。

一昨日→昨日→今日の売上の推移です。「自己相関」で橙色の「一昨日→昨日」と「昨日→今日」のそれぞれのデータの関連性を説明できることを先に紹介しました。

では、一昨日→今日のデータの関連性（緑色）を見たい場合はどうでしょうか？
これを自己相関で見ようとすると、一昨日→今日の間にある「昨日」の時点の影響が含まれてしまいます。

これを取り除き、時点間の直接的な相関を測定できるのが「偏自己相関」です。推移性のある影響を排除し、時点間の関連性を表現することができます。

以上の自己相関関数（ACF）、偏自己相関関数（PACF）を分析して、最適なモデルを識別します。

一般的に、

データが平均値から離れても再び平均値に戻ろうとする「平均回帰性」がある場合はAR項
データにランダムな「ショック」があり、その影響が2つ以上の連続した期間続く場合はMA項

が有効であると言われており、

ACFが徐々に減少し、PACFが特定の時点間で急激に0に近づく場合はARモデル
ACFが特定の時点間で急激に0に近づき、PACFが徐々に減少する場合はMAモデル

が適していると言われています。

ARIMAモデルは以上の流れで最適な（p,d,q）を決定し、構築・選択されます。

ARIMAモデル評価指標調査

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

では、ここまでの内容を踏まえたうえで今回作成したARIMAモデルを評価してみましょう。

ML.ARIMA_EVALUATE関数を使用した下記クエリを実行します。

SELECT
 *
FROM
 ML.ARIMA_EVALUATE(MODEL `yamaguchi_test_bqml.seattle_pm25_xreg_model`)

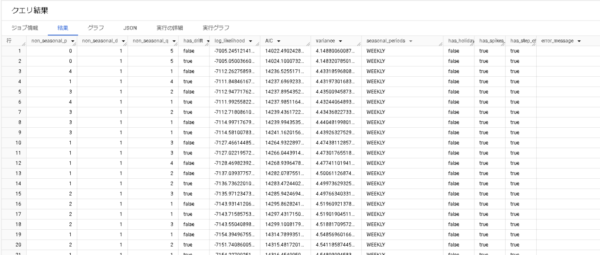
結果には12の列が含まれています。

まず、auto.ARIMAアルゴリズムはKPSSテストと呼ばれる「データの非定常性を確認する」テストを行い、【non_seasonal_d】の値を決定します。
今回はこの値が「1」となっているため、データ内で非定常性が検出され、1回差分がとられています。

その後、先ほど説明した通り【non_seasonal_p（AR項）】、【non_seasonal_q（MA項）】を決定するためのACF、PACF分析が行われます。トレーニングパイプライン内のARIMAモデルは、【non_seasonal_{p,d,q}】、【has_drift】の四つの列で定義されます。今回は42個の候補モデルがトレーニング・検証されていますね。

気になる各候補モデルの性能は、【AIC】列で判断することができます。
AIC：赤池情報量基準とは、統計モデルの予測性の良さを評価する統計量です。

AICが小さいほど当てはまりがよいと言えます。今回はクエリ結果の1行目の組み合わせが採用されています。

ARIMAモデル係数調査

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

次に、今回作成したARIMAモデルの係数を調査します。
ML.ARIMA_COEFFICIENTS関数を使用した下記クエリを実行します。

SELECT
 *
FROM
 ML.ARIMA_COEFFICIENTS(MODEL `yamaguchi_test_bqml.seattle_pm25_xreg_model`)

【ar_coefficients】、【ma_coefficients】列はそれぞれAR項、MA項を指します。どちらも配列で、配列の長さは評価指標で出てきた【non_seasonal_p（AR項）】、【non_seasonal_q（MA項）】です。

今回最も性能の良い（AICが最小の）モデルは(non_seasonal_p , non_seasonal_q) = (0, 5)なので、MA項が有効と判断されているようです。

【processed_input】列には外部変数が表示されており、【weight】列には外部変数がモデルの予測に与える影響の大きさ（重み）が示されています。具体的にみると、

temperature=0.038…（比較的小さな正の値）：気温が上昇するとPM2.5もわずかに上昇する傾向がある
wind_speed＝-1.957…（負の値）：風速が上昇するとPM2.5が大きく低下する傾向がある

ということが考察できます。

【processed_input】列の「__INTERCEPT__」には比較的大きな正の値11.3243…が表示されています。これは他の外部変数の影響を考慮しない場合の予測値のベースラインが高いことを示しています。

ARIMAモデルを使用して時系列を予測する

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

大変お待たせしました。今回作成したARIMAモデルを使って時系列予測してみます。
ML.FORECAST 関数を使用した下記クエリを実行します。

今回、’2020-12-31’までのデータを使ってモデルをトレーニングしているので、’2020-12-31’以降のデータを予測してみます。

SELECT
  *
FROM
  ML.FORECAST( MODEL `yamaguchi_test_bqml.seattle_pm25_xreg_model`,
    STRUCT(30 AS horizon,
      0.8 AS confidence_level),
    (
    SELECT
      date,
      temperature,
      wind_speed
    FROM
      `yamaguchi_test_bqml.seattle_air_quality_daily`
    WHERE
      date > DATE('2020-12-31') ))

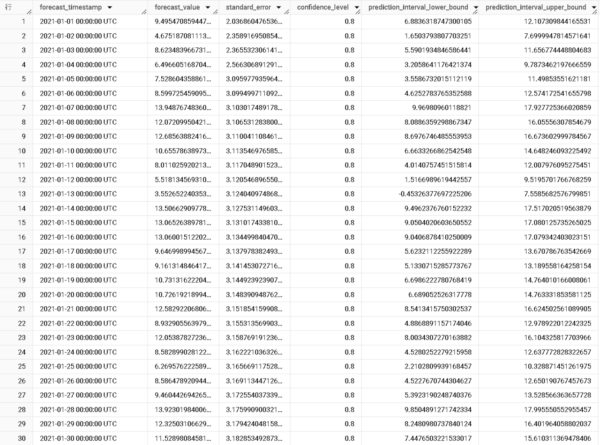
各列の見方は以下の通りです。（今回は箇条書きにします。）

forecast_timestamp：予測対象の日時
forecast_value：モデルによって算出された予測値
standard_error：予測値の標準誤差。大きいほど予測値のばらつきが大きい
confidence_level：予測値の信頼水準
prediction_interval_lower(upper)_bound：予測区間の下限（上限）値。この区間の間に、ある確率（信頼水準）で真の値が含まれると考えられる

1行目のデータを例に見てみます。

このデータは、2021年1月1日の予測値が9.495…であり、80%の確率で真の値は6.883…と12.107…の間にあることを示しています。

実際のデータで予測精度を評価する

シアトルの大気質データからの多変量時系列予測 | BigQuery | Google Cloud

実際のデータを使って、予測の精度を評価します。

ML.EVALUATE 関数を使用した下記クエリを実行します。

SELECT
  *
FROM
  ML.EVALUATE( MODEL `yamaguchi_test_bqml.seattle_pm25_xreg_model`,
    (
    SELECT
      date,
      pm25,
      temperature,
      wind_speed
    FROM
      `yamaguchi_test_bqml.seattle_air_quality_daily`
    WHERE
      date > DATE('2020-12-31') ),
    STRUCT( TRUE AS perform_aggregation,
      30 AS horizon))

時系列モデルに対してML.EVALUATE 関数を使用した場合、下記の指標が得られます。

・mean_absolute_error（MAE）：平均絶対誤差
・mean_squared_error（MSE）：平均二乗誤差
・root_mean_squared_error（RMSE）：二乗平均平方根誤差
・mean_absolute_percentage_error（MAPE）：平均絶対パーセンテージ誤差
・symmetric_mean_absolute_percentage_error（SMAPE）：対称平均絶対パーセンテージ誤差

MAE,MSE,RMSEに関してはこちらのブログをご覧ください。

MAPEは、予測値と実測値の絶対誤差を、実測値で割った値の平均です。相対的な誤差の大きさをパーセンテージで表します。ただし、絶対誤差を実測値で割るため、実測値が0を取り得る場合は使用できません。

SMAPEは、MAPEの改良版で、実測値が0に近い場合に発生する無限大になる問題を改善した指標です。MAPEが上手く機能しない場合はこちらを見ることがあります。

今回の結果のMAE,SMAPEに着目してみると、